PODSTAWOWE INFORMACJE

Funkcja liniowa – funkcja wielomianowa co najwyżej pierwszego stopnia, tj. postaci y=ax+b
gdzie a,b są pewnymi stałymi liczbowymi (parametrami). W artykule rozpatrywane są funkcje zbioru liczb rzeczywistych
w siebie, choć można wykorzystać liczby zespolone. O dwóch zmiennych, z których każda jest funkcją liniową drugiej,
mówi się, że są liniowo zależne lub w zależności liniowej. Nazwa funkcji pochodzi od kształtu jej wykresu, który jest linią prostą daną równaniem y=ax+b. Jednak w algebrze liniowej „liniowość” definiuje nie w oparciu o własności geometryczne,
lecz o własności algebraiczne zachowujące strukturę tzw. przestrzeni liniowych. Funkcje mające tę własność nazywa się przekształceniami liniowymi lub odwzorowaniami liniowymi, a określenie „funkcja liniowa” rezerwuje się dla funkcji opisywanych w tym artykule. Funkcja liniowa jest przekształceniem liniowym, jeśli jest funkcją jednorodną, tj. gdy b=0
mają one wówczas postać proporcjonalności prostej y=ax+b. Funkcje liniowe mają wiele zastosowań związanych z ich regularną strukturą i znanymi własnościami – w szczególności geometrycznymi: korzysta się z nich podczas linearyzacji bardziej skomplikowanych zagadnień, np. przybliżania liniowego; w statystyce korzysta się z metody estymacji (szacowaniu) zależności między dwoma zbiorami danych nazywaną regresją liniową (popularną jej metodą jest metoda najmniejszych kwadratów), w której poszukuje się właśnie zależności będącej funkcją liniową przy jak najmniejszym błędzie standardowym.

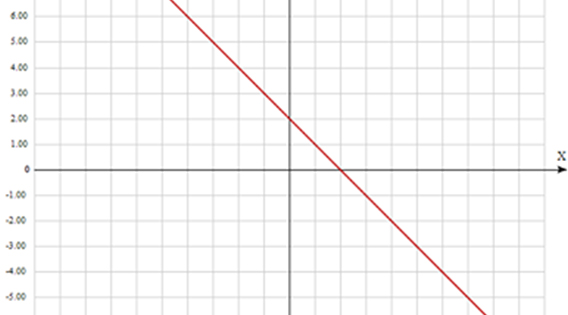
Przykład f(x)=-x+2

Własności:
Jeśli a≠0 to f(x) jest nieograniczona, nieokresowa i monotoniczna:
rosnąca dla a>0 i malejąca dla a<0, ponadto jest różnowartościowa i „na”, a co za tym idzie wzajemnie jednoznaczna.
Jest więc odwracalna (jej funkcja odwrotna również jest liniowa). Jeśli b=0, to f(x) jest nieparzysta.

Jeśli a=0, to f(x) jest funkcją stałą i jako taka jest ograniczona,
parzysta, nie jest również różnowartościowa ani „na”, czyli wzajemnie jednoznaczna. Nie jest więc odwracalna.
Jeśli dodatkowo b=0, to jest jednocześnie nieparzysta.

Jeśli a≠0 to f(x) ma dokładnie jedno miejsce zerowe postaci (-b):a.
Jeśli a=0, to f(x) nie ma miejsc zerowych,
gdy b≠0 i ma nieskończenie miejsc zerowych, gdy b=0.